
La spirale : dans l'histoire, dans la nature, et comme éternelle source d'inspiration dans l'art
Quand j'ai vu les 2 Spirales des 2 côtés de la Ménora de la Synagogue Antique de Priène (Turquie aujourd'hui) et qu'on pense que c'étaient des Rouleaux de la Thora, cela a réveillé ma passion pour la Géométrie.
Plus tard je vis d'autres Ménorot, datant de l'Antiquité à l'Epoque Contemporaine, et, dans plusieurs pays de la Diaspora, cela m'a poussé à réaliser ce travail.

L'article comprend cinq parties
A - La première partie contient plusieurs illustrations de la Spirale dans l'histoire (merci Google). La seconde et la 3e contiennent des méthodes de,
constructions géométriques et l'emploi abusifs de la Spirale Géométrique, la 4 ème contient l'usage de la Spirale pour créer un Modèle, la 5ème contient une série de Modèles créés pour ce travail..
Je me suis abstenu traiter ici, les interprétations liées aux croyances et aux autres interprétations spirituelles et ésotériques.
Voyons d'abord la Spirale dans l'Architecture, les Bijoux, depuis l'Antiquité à nos jours,



Ainsi que dans le monde végétal et le monde animal,


Ainsi que dans l'art décoratif et dans l'art contemporain



 -
-


…et les Tatouages…

-------------------------------------------------------------
B - Seules les spirales géométriques seront traitées. On trouve des spirales de différentes géométries. Leurs dessins de construction se feront à l'aide d'un compas et d'une règle. Mais aujourd'hui l'ordinateur permet d'obtenir des dessins beaucoup plus précis que les instruments Euclidiens. Les dessins ont été réalisés avec le logiciel AUTOCAD-14 (logiciel d'il y a près de 30 ans.) Il est rarement utilisé de nos jours et on a du mal à trouver des techniciens pour vous dépanner. Avec ce logiciel, vous pouvez facilement effectuer toutes les opérations géométriques
- Contrairement au cercle, où, après avoir « marché » sur toute la circonférence, vous vous retrouvez sur le même itinéraire, en spirale , la "marche", vous guide autour du Centre, tout en vous éloignant (ou en vous approchant de ce point). La plupart des modèles que nous présenterons ici, sont basées sur différentes spirales, et les méthodes de leurs constructions. Un travail de manipulation sur la spirale permit de créer des modèles géométriques uniques. Enfin, chaque nouveau modèle est encadré dans un cercle extérieur. .
- Ce chapitre contient quelques genres de spirales et les "Méthodes de leur construction géométrique"
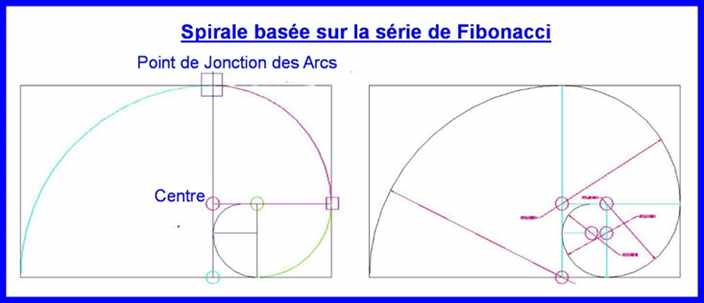
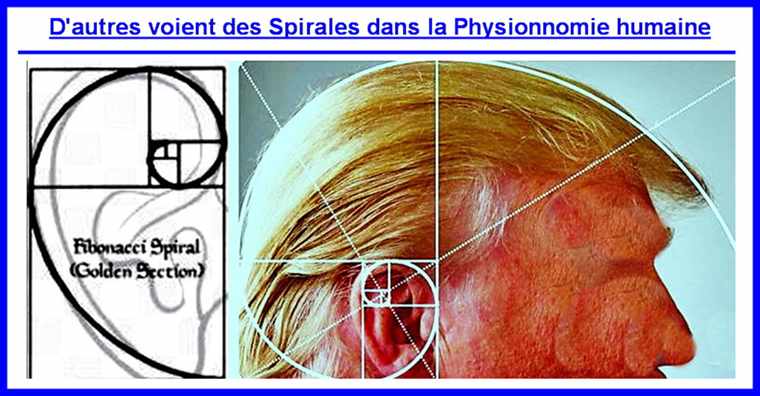
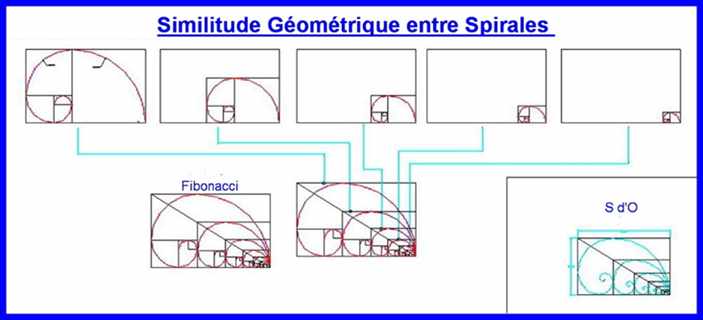
Je pense qu'il a Il y a chez certains auteurs, un abus de "découvrir" partout une spirale basée sur la Section d'Or ou de Fibonacci


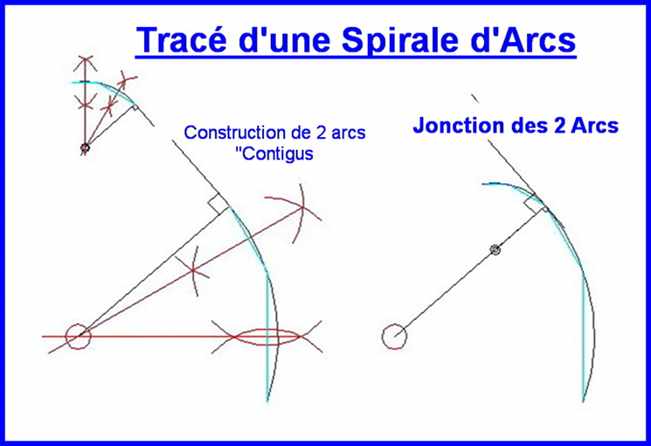
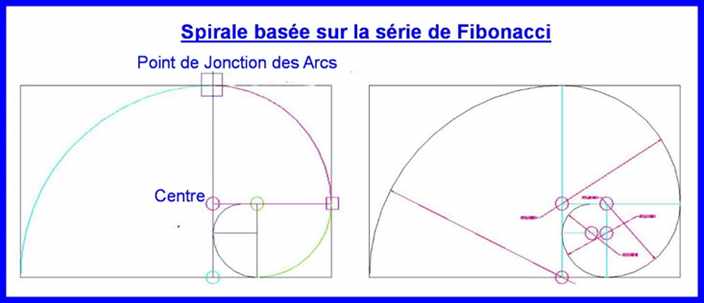
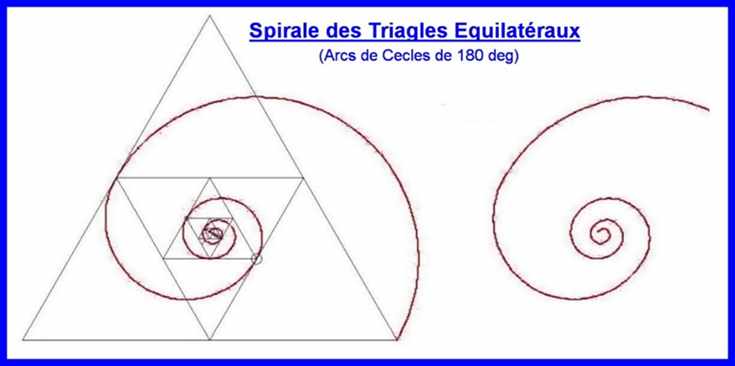
C - La spirale géométrique est constituée d'arcs de cercles qui se connectent pour former une courbe continue, chaque arc est défini par un certain nombre de paramètres : par exemple les coordonnées du centre, le rayon, son point de départ et son angle
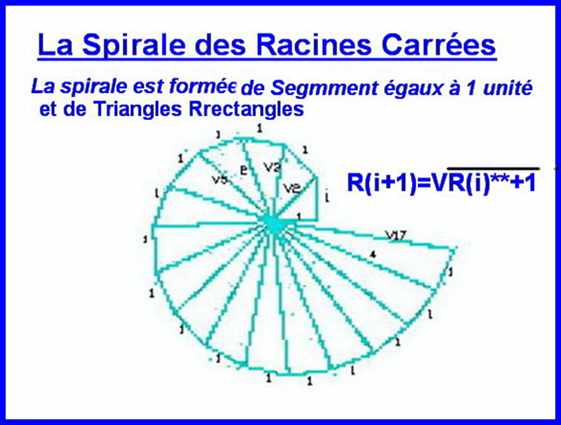
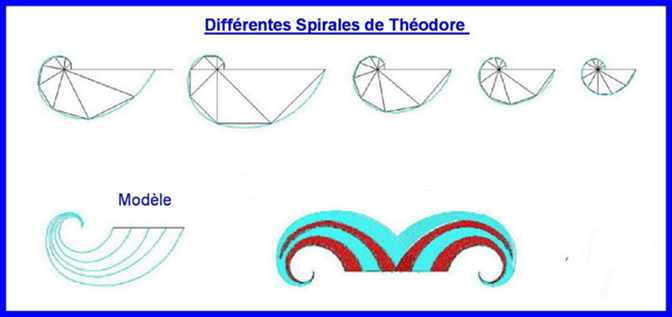
Certaines Spirales sont formées par une courbe qui passe par une suite d'extrémités de lignes brisées (par exemple la spirale "racines carrées", etc.)
La Courbe sera formée des arcs de cercles passant par 3 extrémités de segments à chaque fois, Chaque extrémités de cet arc servira d'extrémité pour l'arc prochain . La continuité de la courbe de la spirale exige que cette extrémité soit sur la ligne qui passe par les centres des Arcs, et ainsi de suite pour toute la spirale
On a vu que la construction de la spirale "des racines carrées" où l'arc de cercle doit passer par les sommets de 2 petits côté (de 2 triangles contigus), donc, par " 3 sommets contigus" à chaque fois, et chaque extrémité de cet arc servira d'extrémité pour l'arc prochain . Cette extrémité devra être en ligne avec les centres des Arcs, et ainsi de suite pour toutes les portions de la spirale.
 -
-
---------------------------------------------------
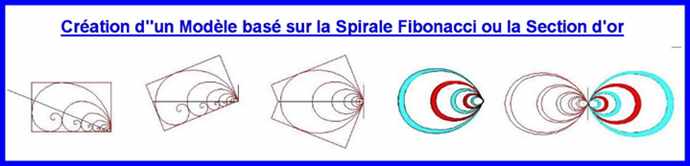
D- Cinq exemples du passage de la Spirale au Modèle final

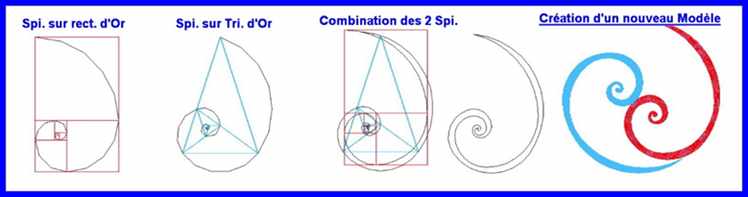



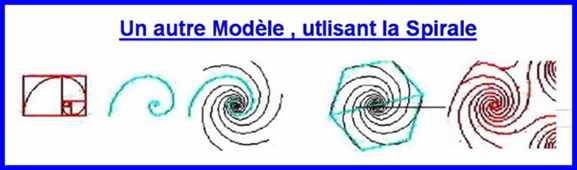


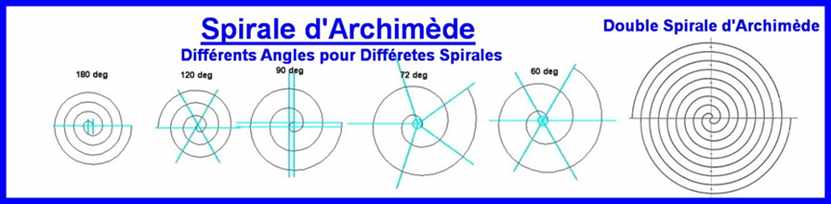
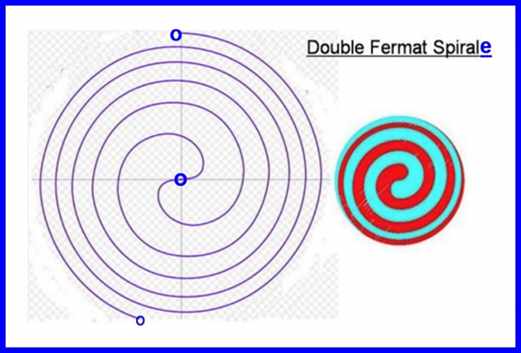
En plus des Genres de Spirales citées jusqu'ici, il y a d'autres, en voici quelques uns:


Abraham Bar-Shay (Ben-Attia)
